Расчет моды и медианы

Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.

Мода - это величина признака (варианта), который наиболее часто встречается в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.

В интервальном ряду распределения мода находится по следующей формуле:

,

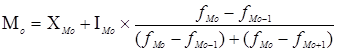где: минимальная граница модального интервала;

- величина модального интервала;

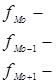{частоты модального интервала, предшествующего и следующего за ним

Модальный интервал определяется по наибольшей частоте. Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и т.д.

Медиана - варианта, находящаяся в середине ряда распределения.

Медиана делит ряд на две равные (по числу единиц) части - со значениями признака меньше медианы и со значениями признака больше медианы.

В случае если вариационный ряд имеет число значений вариант четное, то расчет медианы производится по следующей формуле:

,

где - варианты, находящиеся в середине ряда

В интервальном ряду распределения медиана рассчитывается следующим образом:

,

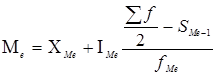где: - нижняя граница медианного интервала;

- величина медианного интервала;

- полусумма частот ряда;

- сумма накопленных частот, предшествующих медианному интервалу;

- частота медианного интервала.

Структурные средние величины (мода и медиана) имеют довольно большое значение в статистике и широкое применение. Мода является именно тем числом, которое в действительности встречается наиболее часто. Медиана имеет важные свойства для анализа явлений: она обнаруживает типичные черты индивидуальных признаков явления, и, вместе с тем, учитывает влияние крайних значений совокупности. Медиана находит практическое применение в маркетинговой деятельности вследствие особого свойства - сумма абсолютных отклонений чисел ряда от медианы есть величина наименьшая:

Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного расположения частот вариационного ряда.

Другое по экономике

Внутренний и внешний долг РФ и его влияние на экономическую безопасность
В современных условиях исполнительной власти для покрытия огромных государственных расходов не хватает налоговых поступлений, а денежная эмиссия ведет к инфляции. Отказ Правительства от использования на эти цели кредитов Центрального б ...